人类视觉系统简直就是一个世界奇迹。看一下接下来的手写体数字序列：

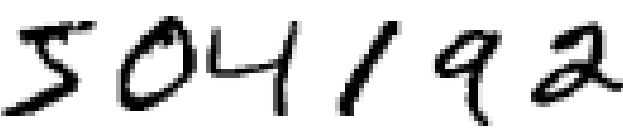
大部分人都能很容易认出这些数字是：504192。你可能觉得这很不靠谱。在我们每个人的大脑中，都有一个初级视觉皮层，也被称为V1。它包含140*10^6个神经元，而这些神经元之间又有百亿种连接。实际上人类视觉活动不是仅仅只有一个V1层，而是由一系列的视觉皮层-V2，V3，V4和V5。这些视觉皮层在逐层地做更复杂的图像处理工作。我们的大脑好比一个超级计算机，通过成千上万年的进化在逐渐地调整参数，来逐渐理解这个可视化的世界。识别手写体数字不是那么容易。我们人类能够很神奇地理解我们的眼睛呈现给我们的，但是基本上这些工作都是在无意识中完成的。当然了，我们通常根本不了解我们的视觉系统在解决多么困难的问题。

如果你想写特定程序来识别上面的这种手写体数字，这会非常困难。而视觉模式识别的困难就像这个例子中的一样。我们自己来识别的时候相当容易，但是在计算机视觉中这却变得异常困难。简单的主观经验告诉我们是如何来识别形状的：“9 有一个圈在上边，一条竖线在右下方”。这在算法上很不容易来表达清楚。你试着来将这些规则（识别手写体数字）精确化的时候，肯定就掉坑里了：不是这里有异常就是那里错误了，还有很多的例外情况—这基本上不太可能。

神经网络用完全不同的方法来解决这个问题。它拿很多的手写体数字（被称为训练集），

之后从这些训练集中学习。换句话说，神经网络使用训练样本来推测规则，进而识别手写体数字。通过增加训练集的数量，神经网络便能够学习到更多关于手写体数字的关系[?]，在这里我仅使用了一百个例子，也许我们可以通过增加上千个甚至百万千万的训练样本来造一个更好的识别系统。

在这一章中我们要写一程序实现神经网络，来通过学习识别手写体数字。整个程序只有74行，没有使用什么特别的神经网络库。但这个程序没有人干预的情况下还是能达到96%的识别率。而且，接下来的一章里我们通过改进算法能够将算法识别率提高到99%。实际上，最好的商业化神经网络已经被用在银行处理支票以及邮政部门识别地址上了。

我们关注手写体识别是因为一般来说它是学习神经网路的非常好的原型问题：极具挑战性；能够识别手写体数字可是不小的成就奥—而且并不要求非常复杂的解决方案或者巨大的计算量。进一步来说，这也是发展更先进技术（比如deepLearning）的好方法。所以本书中我们会不断的返回手写体识别这个问题来进行研究。本书后面，我们会讨论如何将这些思想应用在其他诸如计算机视觉，语音识别，自然语言处理等领域。

当然，如果这一节仅仅是在介绍如何写一段程序来识别手写体，那么这一章本可以很短。但实际上沿着这条思路下来，我们会衍生（develop？）出很多关于神经网络的关键思想，比如两种不同的神经元（感知机和sigmoid 神经元），以及被广泛熟知的标准神经网络学习算法：随机梯度下降算法。自始至终，我都在极力地解释为什么这样来做，并且一直在给大家建立一种神经网络的直观印象。如果我详细阐释基本的概念，这会需要更多的讨论，但是对于你更深层次的理解这些概念还是很有帮助的！最后在本书的最后一章，我们将会理解深度学习是什么，以及为什么它这么重要。

感知器

神经网络是什么？开始我将会解释一种被称为感知器的人工神经元。神经元这一概念最早是由Frank Rosenblatt于1950s到1960s受Warren McCulloch和Walter Pitts的研究所启发而提出的。今天，使用其他的人工神经元模型更为普遍—在本书中以及当前人工神经网络的研究中主要被使用的神经元模型被称为 sigmoid神经元。我们也将会简单讲解 sigmoid 神经元。但为了明白为什么sigmoid 神经元如此定义，还是有必要首先去花些时间来理解感知器。

那么感知器是如何工作的呢？一个感知器接收若干二进制（binary?）输入,然后产生一个二进制输出：

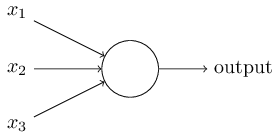
这个例子中的感知器有三个输入,。一般来说它可以有更多或者更少的输入。Rosenblatt提出了一种简单的规则来计算输出—权重：用这些实数来表示各自对应的输入关于输出的重要性（importance?）。输入的加权和大于或者小于阈值（threshold value）决定了神经元的输出是0或1。阈值就像权重一样是个实数，同样也是神经元的一个参数。我们用精确的代数式来表达：

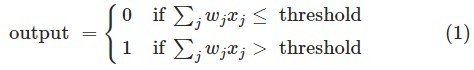
以上便是神经元如何工作的。

上面所述的是基本的数学模型。你也可以把神经元想象成一个通过衡量各种因素后能够做决定的黑箱子。举个不是很恰当但容易理解的例子吧—以后我们会举更多合适的例子。假设你听说这周末长城门票五折（假设你在北京呢），而且你很喜欢装X。心里犯嘀咕去不去呢？你主要想的是下面这几个因素：

1. 天气不知道合不合适？
2. 不知道女（或者男）友想不想陪着你？
3. 那天会不会堵车很严重。

我们可以将这三个因素用对应的二元变量 来表示。举例来说：如果天气好，就令 = 1,否则为 0；同样，女（男）友愿意去就令 = 1,否则为 0；对于堵车也这样来做。

现在假设你特别想去，不管女（男）友愿不愿意陪你去了，也不管堵车怎么回事了。但那天天气真的很重要啊，你总不能冒大雨游长城吧！这时候可以用感知器来模拟这次决策。一种方式是令 = 6来对应天气, = 2和 = 2 来对应女（男）友和交通情况。最大值 表示天气因素要比其他两种情况影响大。最后（假设）你选择阈值为5。最后这个神经元运行决策模型的时候，如果天气好，它就输出1，反之输出0。你会发现输出和女友愿意与否，交通情况没有什么关系。

通过给阈值和权重设置不同的值，我们能够得到不同的决策模型。举例来说，令阈值为3。你会发现天气好或者女友愿意，交通也好都会导致输出为1。换句话说，它是一个不同的模型。减少阈值意味着你更倾向于去长城。

很明显，感知器不是一个完整的人类决策模型！但上述例子阐释了感知器如何衡量不同因素后做出决策的。下面由很多感知器组成的复杂网络似乎可以做出精细的决定：

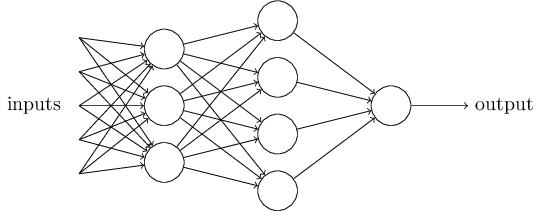
在这个网络中，第一列感知器们我们称为第一层—通过对输入进行加权它做出三个简单的决定（is making three very simple decisions）。第二层中每个感知器通过对上一层感知器的输出结果加权后做出决定。通过这种方式第二层的感知器能够在比第一层的感知器更加复杂的和抽象的层面上做出决策。第三层的感知器甚至能做出更加复杂的决定。这样下去，多层感知器网络就可以做出复杂的决策。

顺便说一句，我们在这里定义的感知器仅有一个简单的输出。上面的这个感知器网络似乎有很多输出，实际上它们还是只有一个。上面的感知器的多路输出的箭头仅仅是表示这层感知器被下一层的多个感知器所使用。这样画肯定比画一条线（输出）然后再分裂为多个显得简洁。

简化对感知器的描述。 显得相当麻烦，这里对符号进行两处变换。第一处是将换成点积形式：,这里和分别是权重和输入的向量形式。第二处变换是将阈值移到等式的左边，也即用感知器中常见的概念偏差（bias）来代替：。这样感知器可重写为如下形式：

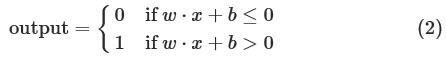
你完全可以将偏差理解成感知器输出1的倾向程度。或者从生物学角度这么理解吧，偏差是衡量一个感知器被激活的难易程度。对于一个有较大偏差的感知器，它非常容易输出1。但是如果偏差是负的，感知器便很难输出1了。很明显，引入偏差对在描述感知器简洁性方面影响不大，但是之后我们会发现这样做使得代数式会更加简洁。正因如此，以后书中我们都会将阈值用偏差来代替。

以上我们将感知器描述成衡量各种因素后做出决策的决策箱。感知器另外一种用处就是对基本的像 “与”，“或”和“与非”这样的树立逻辑函数进行运算。举个例子，假设某感知器有两路输入，权重均为-2，整体偏差是3。如下：

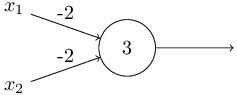
我们会发现00 输入产生了输出1，因为（-2）0+（-2）0+3=3 是正的。这里我们引入符号* 使该乘法显式化。相同的计算表明 输入01 和10 都会产生同样的输出1。但是输入11 却产生输出0，因为 (−2)∗1+(−2)∗1+3=−1 是负的。通过以上分析我们知道这个感知器的作用是一个“与非”门。

这个“与非”门的例子说明我们可以使用感知器计算简单逻辑函数。实际上我们可以使用感知器网络计算任意的逻辑函数。因为“与非”门在计算中非常普遍，所以我们可以使用“与非”门构建任意计算。举个例子，我们使用若干“与非”门来组建一个电路对 和相加。这就需要计算的逐位相加和，以及进位（当和都是1时，要进1 ）。进位位正好是:

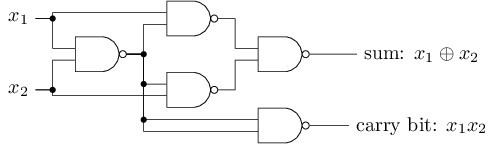
如果将上述电路转化为等价的感知器网络，就需要将所有的“与非”门替换为两路输入的感知器，每个感知器的权重为-2，偏差为3。下面就是替换后的网络。注意，这里我将右下方的“与非”门替换为对应的感知器，使得这个图上的箭头容易画

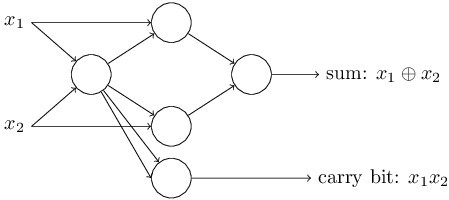
需要注意的一点是这个感知器网络最左边的感知器的输出对应予最下面的感知器的输入被应用了两次。当我们定义感知器模型的时候并没有清楚的指明一个地方到另一个地方的双路是否可以有两次。实际上这并不重要。如果我们不允许这样的事情（一个地方到另一个有两路输出），这里完全可以把两条权重为-2的线简化为一条权重为-4的线。（要是你还没有明白为什么可以这样，最好停下来自己证明一下这是等价的）这样简化后，网络看上去是这样子的：没有标记的权重是-2，所有的偏差是3，标记的那个单一的权重是-4。

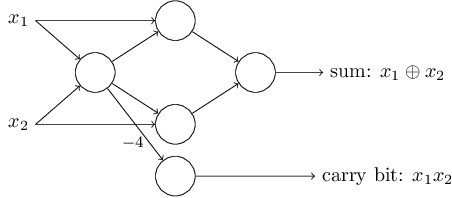
现在，我已经将像这样的两个变量画在了感知器网络的最左边。实际上，传统上我们再画一层额外的感知器—输入层—来编码输入。

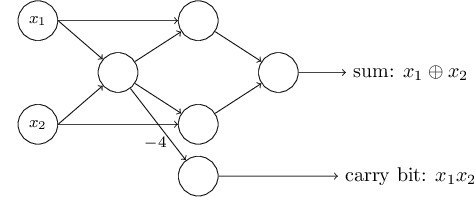
这个输入感知器算式没有输入只有输出，算是一种速记法

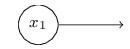
它并不是没有